Definition
The phenomenon of raising outer edge of the curved road above the inner edge is to provide necessary centripetal force to the vehicles to take a safer turn and the curved road is called Banking of Roads.
Introduction
When a vehicle goes round a curved road, it requires some centripetal force. While rounding the curve, the wheels of the vehicle have a tendency to leave the curved path and regain the straight line path. Force of friction between wheels and the roads opposes this tendency of the wheels. This force of friction therefore, acts towards the centre of circular track and provides the necessary centripetal force.
Banking of Roads is a common topic in physics homework, often involving calculations related to centripetal force and friction. Students frequently encounter challenges understanding the principles and equations that describe how banking helps vehicles maintain traction and stability on curved paths.

Fig. (1) Vehicle moving on level road
In fig (1), it is shown that a vehicle of weight ‘mg’ (acts vertically downwards) is moving on a level curved road. R1 and R2 are the forces of normal reaction of the road on the wheels. These are vertically upward since road is leveled. Hence,
R1 + R2 = mg
Let F1 & F2 are forces of frictions between tyre and road directed towards centre of curved road.
∴ F1 = μ R1
And
F2 = μ R2
where μ is coefficient of friction between tyres and road.
If ‘v’ is the velocity of the vehicle while rounding the curve, the centripetal force required is mv²/r. As this force is provided by the force of friction therefore

Hence the maximum velocity with which a vehicle can go round a level curve; without skidding is
![]()
Banking of Roads
In the above discussion, we see that the maximum permissible velocity with which a vehicle can go round a level curved road depends on μ, the coefficient of friction between tyres and road. The value of μ decreases when road is wet or extra smooth or tyres of the vehicle are worn out. Thus force of friction is not a reliable source for providing the required centripetal force to the vehicle. Especially in hilly areas where the vehicle has to move constantly along the curved track, the maximum speed at which it can run will be very low. If any attempt is made to run it at a greater speed, the vehicle is likely to skid and go out of track. In order that the vehicle can go round the curved track at a reasonable speed without skidding, the sufficient centripetal force is managed for it by raising the outer edge of the track a little above the inner edge. It is called banking of the circular track or Banking of Roads.
Consider a vehicle of weight ‘Mg’ moving round a curved path of radius ‘r’ with speed ‘V’ on a road banked through angle θ. If OA is banked road and OX is horizontal line, then ∠AOX = θ is called angle of banking of road. Refer Fig (2)

Fig.(2) Vehicle moving on Banked Road
Following forces are involved:
- The weight ‘Mg’ acting vertically downwards
- The reaction ‘R’ of the ground to the vehicle acting along normal to the banked road OA in upward direction
- The vertical component R.Cos θ of R will balance the weight of the vehicle.
- The horizontal component R.Sin θ of R will provide necessary centripetal force to the vehicle.
Thus,
R.cos θ = Mg ….(1)
And
![]()
On dividing equation (1) & equation (2),we get

Knowing ‘v’ and ‘r1’, we can calculate θ. If ‘h’ is the height AX of outer edge of the road then from fig.(3),
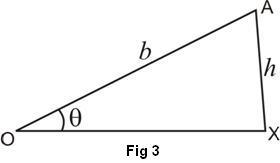
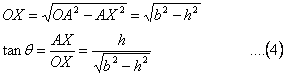
From equations (3) & (4) we get
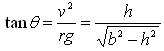
From above eqn. we can calculate h. usually h < < b. Therefore. h2 is negligible, hence
![]()
Roads are generally banked for the average speed of vehicles passing over them. However, if the speed of a vehicle is somewhat less or more than this, the self adjusting state friction will operate between tyre and road and vehicle will not skid.
References
- Modern’s ABC of Physics (XI)
- Pradeep’s Fundamental Physics (XI)
